Faculty of Medical and Health Sciences
Department of Pharmacology & Clinical Pharmacology, University of Auckland Faculty of Medical and Health Sciences
Department of Pharmacology & Clinical Pharmacology, University of Auckland

Ligand Binding

[Hide side menu]

Objective and introduction

Objectives

The objectives are:

  1. Understand the properties of binding sites and receptors that can be modelled quantitatively.
  2. Define equilibrium ligand binding models in terms of unbound ligand concentrations.
  3. Understand how total ligand concentrations can be used to predict unbound ligand concentrations.

Introduction

The study of ligand binding is an essential step in identifying receptor binding sites. There are several methods for analysing ligand binding experiments. This laboratory offers the opportunity to compare the most widely used. Ligand binding models describe the interaction of one or more ligands with one or more binding sites. Binding sites can be described by their behaviour as being saturable or non-saturable. Saturable binding is also called specific binding and non-saturable binding is also called non-specific binding. Receptors have saturable binding sites and also express an effect. Models for ligand binding are based on the law of mass action. Models can describe the time course of binding (association and dissocation) but more commonly binding is described at equilibrium. The driving force for binding is the unbound ligand concentration but experimentally only total ligand concentrations can be varied. Measurements of bound ligand can be used to predict unbound ligand concentration (unbound=total-bound) but the measurement error in the bound concentration will influence the predicted unbound concentration.

Pharmacometrics uses mathematics and techniques of regression to describe, explain and predict the relationships of variables within biological systems. In addition to pharmacological systems, these modelling methods can be applied to physiological systems. Ligand binding models in particular have broad applications and can used to describe processes in endocrinology and biochemistry, including experiments with neurotransmitters, and radioimmunoassays. Ligand binding analysis is necessary to identify receptor binding sites in drug development.

Ligand binding models describe a system of interacting components. A ligand is something that binds to a binding site. Binding is association of a ligand to a binding site, and is determined by the unbound ligand concentration and the physiochemical properties of the binding site (the affinity of the site). Multiple ligands and multiple binding sites can be simultaneously described using ligand binding models. Binding sites may be saturable (specific binding) or non-saturable (nonspecific binding). High concentrations of ligand added to a binding system produce binding, particularly nonspecific binding. Nonspecific binding is linearly proportional to unbound ligand concentration. Many biological tissues have both saturable and non-saturable components. Binding does not always produce an effect. Receptors are saturable binding sites that express an effect.

The law of mass action describes the equilibrium between association and dissociation of ligands with binding sites.

Binding site + Cu ←→ Cb-Binding site i.e. Unbound Receptor + Unbound Drug ←→ Receptor-Drug Complex

Although binding is modelled primarily in terms of the concentrations of the ligand (bound, unbound, total), the amount of unbound binding site influences binding. And this becomes important in understanding the interactions between multiple ligands and multiple binding sites. It is the interaction between these multiple components requiring complex forms of nonlinear regression, which can be difficult to understand intuitively and mathematically.

At equilibrium

Koff.(CRbound) = Kon.(Cu).(Runbound)

Koff describes the dissociation of ligand binding
Kon describes the association of ligand binding
Kd is the equilibrium dissociation constant and equal to Koff/Kon.

The fraction of binding sites occupied by the ligand is mathematically described as follows:

Occupancy = Cu/(Kd+Cu)

Binding sites with high affinity (low Kd) for a ligand bind low concentrations of ligand (and vicaversa). The concentration of unbound ligand (Cu) is the driving force for binding, and defines equilibrium. Bound (Cb) and unbound concentrations of ligand make up the total concentration of ligand (Ct). In theory, bound, unbound or total concentrations could be measured for some systems depending on the systems properties or the experimental design. Unbound concentrations can be predicted from either total or bound concentrations. Where there are multiple ligands and multiple binding sites the binding of all ligands must be known in order to predict unbound concentration.

Different ligand binding models and methods of analysing and predicting ligand binding have been developed. Families of sigmoid curves describing binding models can be analysed simultaneously and the parameters of each component can be estimated. Complex interactions between ligands that displace each other can be modelled. Saturation experiments by design measure a large range of bound concentrations, which can make the results difficult to appreciate graphically. Displacement experiments usually result in a smaller range of bound concentration measurements. Saturation experiment observations of bound concentration can be transformed into displacement observations simplifying the error model.

The simplest form of Ligand binding model has a similar mathematical form to the Emax model.

One Ligand, One binding site:

B = Bmax * Cu/(Kd+Cu) + NS*Cu

This simple model can be extended for multiple binding sites or ligands, as long as additional parameters are added.

The parameters are as follows:

Equilibrium dissociation constant Kd concentration at which binding site is 50% occupied.
One for each ligand-binding site combination.
Affinity 1/Kd  
Binding Capacity Bmax concentration of the binding site
One for each binding site
Nonspecific binding NS proportionality constant (slope)
One for each ligand

Graphical models of binding usually represent Cb versus Cu, or Cb versus Ct reflecting the relationship of these variables at equilibrium; rather than depicting the time course of association and dissociation). Initial parameter estimates can be made from graphs of Cb versus Cu, or Cb versus Ct. Bmax is estimated from the plateau or maximum of saturable binding (similar to initial estimates of Emax), and Kd from the Cu at which the binding site is 50% occupied (similar to initial estimates of EC50). Nonspecific binding is estimated from the slope of the nonsaturable part of the binding curve.

The relationship between the variables is somewhat complex, as the variables Cb and Cu are not independent of each other. By convention Cb is usually displayed on the Y axis, and Cu or Ct on the X axis. Usually a combination of Ct and either Cb or Cu are measured, with the remaining variable calculated. Occupancy = Cu/(Kd + Cu)

Linear and nonlinear methods can be used to analyse ligand binding. Sophisticated and ‘naive’ approaches are possible. The two commonest approaches are the Naive unbound method, and the Predicted Unbound method. The Naive unbound method calculates Cu from Ct, but incorporates measurement error from Cb. The predicted unbound method is more precise and predicts Cb using Ct (quadratic equations). Non specific binding concentration is calculated by subtracting specific binding from total binding.

Introduction by Anita Sumpter (2008).

Theory

Saturable Binding

The binding of a ligand to a single binding site is definable by the concentration of the binding site (Bmax) and the concentration of unbound ligand at which the binding site is 50% occupied (Kd). The Kd is also known as the equilibrium dissociation constant. Its reciprocal is a measure of affinity.

Non-Saturable Binding

Ligand binding to non-saturable sites is more accurately called non-saturable binding but it is also known as non-specific binding. By definition non-saturable binding is always linearly proportional to unbound ligand concentration. The proportionality constant (slope) has the symbol NS.

The binding of a ligand to a biological tissue will usually have both specific and non-specific components and can be described by the following model:

 

Equation 1

When there is more than one binding site or more than one ligand the same basic model can be extended. There is always a Bmax for each site, a NS for each ligand and a Kd for each site•ligand combination. For one ligand, L, binding to two specific sites:

 

Equation 2

If a second displacing ligand, D, is added then the model for the binding of L to one binding site is:

 

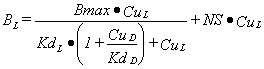Equation 3

For two binding sites and two ligands, L and D, the binding of L is:

 

Equation 4

Note that the unbound concentration of each ligand is needed to predict the binding. Usually experiments are designed using accurately known total ligand concentrations and measurements are made of the bound ligand. The binding of all the ligands in the system must be known to predict the unbound concentration. This can be done using a general binding model described by Feldman (1972) and implemented by Munson & Rodbard (1980). This model is implemented in the BIND library in MKMODEL.

  • Feldman HA. Mathematical theory of complex ligand-binding systems at equilibrium. Analyt Biochem 1972; 48:317-338
  • Munson PJ, Rodbard D. LIGAND: A versatile computerised approach for characterisation of ligand binding systems. Analyt Biochem 1980; 107:220-239

Binding Experimental Design 

There are two basic designs for binding experiments:

  1. Saturation
    Increasing concentrations of the primary ligand are added to the system. Low concentrations are in the range of the Kd and high concentrations are much higher and approach saturation of the binding site. However, the high concentrations produce binding which is usually dominated by the non-specific component. The range of bound concentration measurements is often over several orders of magnitude.
  2. Displacement
    A fixed concentration of a primary ligand (usually radioactive i.e. "hot") is added to the system and increasing concentrations of a displacing ligand (usually non-radioactive i.e. "cold") are used to displace the primary ligand. The primary and displacing ligands can isotopes of the same molecule or different molecules. The range of bound concentration measurements is usually over less than one order of magnitude.

Transformation of Saturation to Displacement

It is useful to appreciate that simple saturation experiment observations can be transformed into equivalent displacement experiment observations. This transformation reduces the range of bound concentration measurements which makes it easier to appreciate the binding curve graphically and simplifies the error model. The transformation is performed by imagining that the total ligand in the saturation experiment is divided into a radioactive "hot" part and a non-radioactive "cold" part. The "hot" concentration is chosen to be smaller than the lowest total ligand concentration. The concentration of "hot" ligand will be proportional to its concentration so that the transformed bound concentration is obtained from:

Bounddisp = Boundsatn/Totalsatn • Hotdisp

The concentration of cold ligand in the equivalent displacement experiment is:

Colddisp = Totalsatn - Hotdisp

Workshop tasks

One Ligand, One Binding Site

Table 1 shows the binding of a drug to plasma proteins. Ct is the total drug concentration measured in plasma. Cu is the concentration of unbound drug measured after equilibrium dialysis. Cb is the concentration of bound drug obtained by subtracting Cu from Ct.

Ct Cu Cb
0.01210 0.01059 0.00150
0.03626 0.02899 0.00727
0.1206 0.1021 0.0185
0.3596 0.3048 0.0548
1.177 0.9946 0.1821
3.405 2.931 0.4745
5.550 4.900 0.6499
10.77 10.01 0.7537
31.16 30.32 0.8385
102.0 100.0 1.904
 Table 1. Binding of a drug to plasma proteins.

Visual Method

Find the file Pharmacometrics Data\Ligand Binding\bind1.xlsx

  1. Open bind1.xlsx in Excel.
  2. Create scatter plots of Cu versus Cb and Ct versus Cb.
  3. Estimate Bmax, Kd and NS from the graph.

Naive Unbound Method (L1S1N)

  1. Export the binding data from bind1.xlsx to .csv format (bind1.csv) and save in your Ligand Binding folder. Remember to add an #ID column so that MONOLIX can read the file.

    The column headers for all data files will be:

    #ID Ct Cu Cb
  2. Open Monolix and create a
     
    New Project.
  3. In Monolix, click 'The data', locate your bind1.csv file and click open. Do not use the default header. Instead, specify the ID column, set Ct to IGNORE, set Cu to REGRESSOR (scroll down to find) and Cb to OBSERVATION.
  4. Use a text editor to create the L1S1N model. Start by opening a text editor (e.g. Editplus) and enter the code shown in Figure 1.

    ; Naïve Unbound Model L1S1N - One Ligand One Site binding using measured bound

    INPUT:
    parameter={bmax,kd,ns}
    regressor={cu}

    EQUATION:
    cb=bmax*cu/(cu+kd)+ns*cu

    OUTPUT:
    output = {cb}


     Figure 1. Code for L1S1N_mlxt.txt

    IMPORTANT: MLXTRAN is case sensitive. Please take care with variable names.

  5. Save the model as L1S1N_mlxt.txt in your Ligand Binding folder.
  6. Click 'The structural model' and the model library will appear. Click 'Browse and navigate to your Ligand Binding folder and click 'OK'. Select L1S1N_mlxt.txt and click 'OK''.

    If you get a compile error. Double check that your code is identical to that shown in Figure 3 and be sure there is a blank line after the last line of code - this is required to 'end' the last statement.

  7. Click on 'Initial parameter estimates' and change to reasonable starting values based on the plots of cu vs cb and cu vs ct.
  8. Set the 'Std. deviations.' to 0 and use the settings cogwheel symbol to fix the value for each of the parameters to a constant value.

    Because these are data from a single individual, there is no between subject variability (random effects). The SD of random effects is therefore 0.

  9. Set the 'Residual error parameters' to 1 (a) (additive)  and 0.1 (b) (10% coefficient of variation) and 1 (c)  for the bound concentration observation. Fix parameter C to a constantt value.
  10. Click 'Check initial fixed effects'. A plot of predictions based on the model and initial parameter estimates will display along with the observed values. Close the 'Check initial fixed effects' window.

    When you have chosen initial estimates that form a prediction that is similar to the observations.

  11. Go to the 'Statistical Model & Tasks' window.
  12. Click on STANDARD ERRORS and LIKELIHOOD so that the check mark shows.
  13. Set the ERROR MODEL to COMBINED1
  14. Click on 'None" under RANDOM EFFECTS.
  15. IMPORTANT: Save the project as L1S1N_project.mlxtran in your Ligand Binding folder.
  16. Estimate the parameters by clicking on Run. This will take a while depending on the complexity of the model. During the estimation process you can see how the parameter estimates are being changed and settle down towards the final value.
  17. Look at the Individual fit and save a pdf copy in your L1S1N project folder.
  18. Look at the VPC plot then click on Settings, use the default settings and add 'Individual Data'. Then click on 'Bins and CI' at the bottom of the list of options. Click on 'Equal width' and then click on 'Display'. Save a pdf copy of the VPC plot in your L1S1N project folder.
  19. View the parameter estimates by clicking
     
    'Last Results'. A text file containing these results is saved as 'pop_parameters.txt' in the project folder.
  20. IMPORTANT: Save the project again as L1S1N_project.mlxtran in your Ligand Binding.

Predicted Unbound Method (L1S1)

Instead of using the measured (with error) value of Cb to calculate Cu from Ct, it is more precise to predict Cb using Ct. Algebraic rearrangement of the one binding site model after substitution of Cu with the expression Ct-Cb leads to a quadratic function of Cb:

 

Equation 5

where the coefficients a, b and c are defined in terms of Ct and the binding model parameters Bmax, Kd and NS.

 

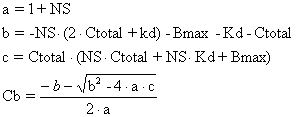Equation 6

The model prediction for Cb is then obtained using the standard formula for finding the (positive) root of a quadratic equation.

  1. Use a text editor to create the L1S1 model shown in Figure 2.

    ; Predicted Unbound Model L1S1 - One Site binding using predicted bound

    INPUT:
    regressor={ct}
    parameter={bmax,kd,ns}
    EQUATION:

    a=1+ns
    b=-ns*(2*ct+kd)-bmax-kd-ct
    c=ct*(ns*ct+ns*kd+bmax)
    cb=(-b-sqrt(b*b-4*a*c))/(2*a)

    OUTPUT:
    output={cb}

     Figure 2. Code for L1S1_mlxt.txt
  2. Save as L1S1_mlxt.txt in your Ligand Binding folder.
  3. In Monolix, select the new model, compile it and accept it for use.
  4. Click 'The data'. Specify the ID column, set CT to REGRESSOR, set CU to IGNORE and CB to OBSERVATION.

    NOTE: CT is now the independent variable. NOT CU.

  5. Save the project as L1S1_project.mlxtran in your Ligand Binding folder.
  6. Run the model and look at the results as you did for L1S1N.

One Ligand, Two Binding Sites

Visual Method

Find the file Pharmacometrics Data\Ligand Binding\bind2.xlsx

  1. Open bind2.xlsx in Excel.
  2. Look at the bind2 worksheet.
  3. Create scatter plots of Ct versus fb and Cu versus Cb.
  4. Estimate bmax1, bmax2, kd1, kd2 and bs from the graphs.

    Hint: Use the plot of  Ct vs fb with plots of Cu versus Cb using 0-100 and 0 to 100000 for the Cu axis.

Naive Unbound Method (L1S2N) Using Fraction Bound

  1. Press the F9 key until the graph on the bind2 sheet approximately resembles the graph in the simulation sheet in bind2.xlsx.
  2. Export the binding data from the bind2 sheet in bind2.xlsx to .csv format (bind2.csv) and save in your Ligand Binding folder. 
  3. In Monolix, click 'The data', locate your bind2.csv file and click open. Specify the #ID column, set CT to REGRESSOR, set CUN to REGRESSOR, set CB to IGNORE and set FB to OBSERVATION..
  4. Use a text editor to create the L1S2N_FB model shown in Figure 3.

    ; Naive Unbound Model L1S2N - fraction bound
    ; Two binding site One Ligand Naive unbound model

    INPUT:
    parameter={bmax1, bmax2, kd1, kd2, ns} ; binding parameters
    regressor={ct,cu} ; total and unbound conc

    EQUATION:
    cb=bmax1*cu/(cu+kd1)+bmax2*cu/(cu+kd2)+ns*cu
    fb=cb/ct

    OUTPUT:
    output = {fb}

     Figure 3. Code for L1S2N_FB_mlxt.txt
  5. Save the model as L1S2N_FB_mlxt.txt in your Ligand Binding folder.
  6. In Monolix, select the new model, compile it and accept it for use.
  7. Enter your initial parameter estimates for bmax1, bmax2, kd1, kd2 and ns under Fixed effects.
  8. Use a combined ("combined1") residual error model with an inital estimate of 0.01 for 'a' and 0.01 for 'b' (used to simulate Cb).
  9. Then try using additive ("constant") residual error model with initial estimate of 0.1 for 'a' (more reasonable for Fb).
  10. Save the project as L1S2N_FB_project.mlxtran in your Ligand Binding folder.
  11. Run the model and look at the last results and graphical output.

Learning

  1. Use the internet to search for a review on ligand binding data analysis. Comment on the recommended methods for analysis.
  2. What are the problems associated with Scatchard's method (transformation of bound and unbound concs to linear form)?

    Hint: You may find Saturable Binding Data a useful place to start your reading.

Use the internet to search for software for ligand binding analysis. Pay particular attention to finding methods that use Feldman's simultaneous equation method as initially implemented by Munson & Rodbard in their BASIC program LIGAND.