Non-linear PK
Objective and introduction
Objective
The objectives are to
1. learn about non-linear elimination models using Excel, Berkeley Madonna, Monolix and NONMEM, and
2. compare Euler and RungeKutta differential equation solvers.
Introduction
Describing
and quantifying drug
elimination is a key component of pharmacokinetics. The term ‘drug
elimination’
describes irreversible loss of the drug from the body. Generally, renal
excretion and hepatic metabolism are the primary ways through which
drugs are
eliminated, with hepatic excretion (through the bile) also important
for some
drugs. For some drugs, elimination may be independent of both liver and
kidneys. Remifentanil, an opioid used for analgesia during surgery, is
eliminated via metabolism by plasma esterases. Other more complex
pathways also
exist for elimination, such as internalisation of drug-bound receptors
or
clearance via endocytosis. These are often termed ‘nonspecific
clearance’. Non-linearity
may also apply to other processes relevant to PK, including absorption
and
distribution.
Clearance and first-order elimination
Clearance
(CL) describes the
relationship between the rate of drug elimination and drug
concentration e.g.
| Rate of elimination = CL x Cp | Equation 1 |
where
Cp is the plasma drug
concentration. CL is important clinically because it determines the
average
concentration achieved at steady state given a particular input rate,
and the
maintenance rate required to maintain steady state during repeat
dosing. For
most drugs, clearance is constant under normal conditions and
independent of
concentration and dose, although it may change due to disease,
pregnancy or
other factors. CL has units of L/h (or volume/time) and is defined as a
‘proportionality
constant’ because it describes the proportional change in elimination
rate with
concentration. Depicted graphically this relationship is linear, or
‘first-order’,
with CL equating to the slope of the line. Many people confuse CL and
elimination
rate as being the same thing, but they are not.
| CL = Q x ER | Equation 2 |
| ER = (Ca-Cv) / Ca | Equation 3 |
In
the above equations, Q denotes
blood flow to the organ, Ca is concentration in
the arterial vessels
delivering drug to the organ, and Cv is the
concentration in the
venous vessels transporting drug from the organ to the rest of the
body. The
difference between Ca and Cv
represents drug loss through
elimination at the organ. The ability of an organ to clear drug is
dependent on
its intrinsic clearance and blood flow to that organ (Q). Clearance by
several
organs is additive, e.g.
| CLTOTAL = CLHEPATIC + CLRENAL + CLOTHER | Equation 4 |
Nonlinear Elimination
Many
of the processes involved in
drug absorption, distribution, metabolism and excretion are first-order
processes but can become saturated at high drug concentrations. This
occurs
when the transporters or enzymes integral to the reaction are
predominantly all
taken up by their substrate so there are few free transporters or
enzymes
available. Saturation may also occur due to depletion of cofactors.
This
results in non-linear or ‘mixed-order’ kinetics. Passive diffusion
across cell
membranes and filtration of drug at the glomerular are examples of
non-saturable processes where irrespective of drug concentration, a
first-order
relationship exists.
Nonlinear elimination is most often
seen metabolic processes. Metabolism is a capacity limited reaction
where the amount
of enzyme or co-factor limits the rate of reaction, and can be
described by the
Michaelis-Menten equation:
| V = (VMax · C)/ (KM + C) | Equation 5 |
In Equation 5 V is the velocity of the reaction, Vmax the maximum velocity, C the concentration of the substrate, and Km is the Michaelis-Menten constant. The reaction between enzyme and substrate (drug) is depicted below in Figure 1. When the concentration of the substrate is low relative to Km, Km+C ≈ Km. Here the denominator of Equation 5 simplifies to Km and a linear relationship exists where the rate of the reaction varies proportionally (by a constant, Vmax/Km) with concentration. This is a first-order relationship. The ratio of Vmax/Km is a constant and is equivalent to the term clearance used when elimination is first-order. When concentrations are large relative to Km, Km+C ≈ C. In this context, the denominator of Equation 5 simplifies to C and the equation approximates Vmax (see Equation 6). Here saturation has occurred, there are no further increases in rate with increasing concentration and the kinetics are zero-order (constant) with the rate of elimination equal to Vmax. This cannot happen in reality because C must be infinite to truly achieve zero-order elimination. In this context we see mixed order, or nonlinear, elimination (Figure 2).
V ≈ (VMax · C)/ C ≈ VMax |
Equation 6 |
Figure 1. The metabolism of a substrate (S) by an enzyme (E). The association of S + E is described by the rate constant K1 with units of 1/concentration.1/time. An intermediary complex S-E is formed. This is reaction is reversible. While associated with S, E is occupied and taken out of the free enzyme concentration available to act on other S molecules. The rate constant Kcat describes the rate of enzymatic conversion forming the product of metabolism P and releasing E to act on further S molecules. K2 and Kcat have units of 1/time. Km, the Michaelis-Menten rate constant, has units of concentration.
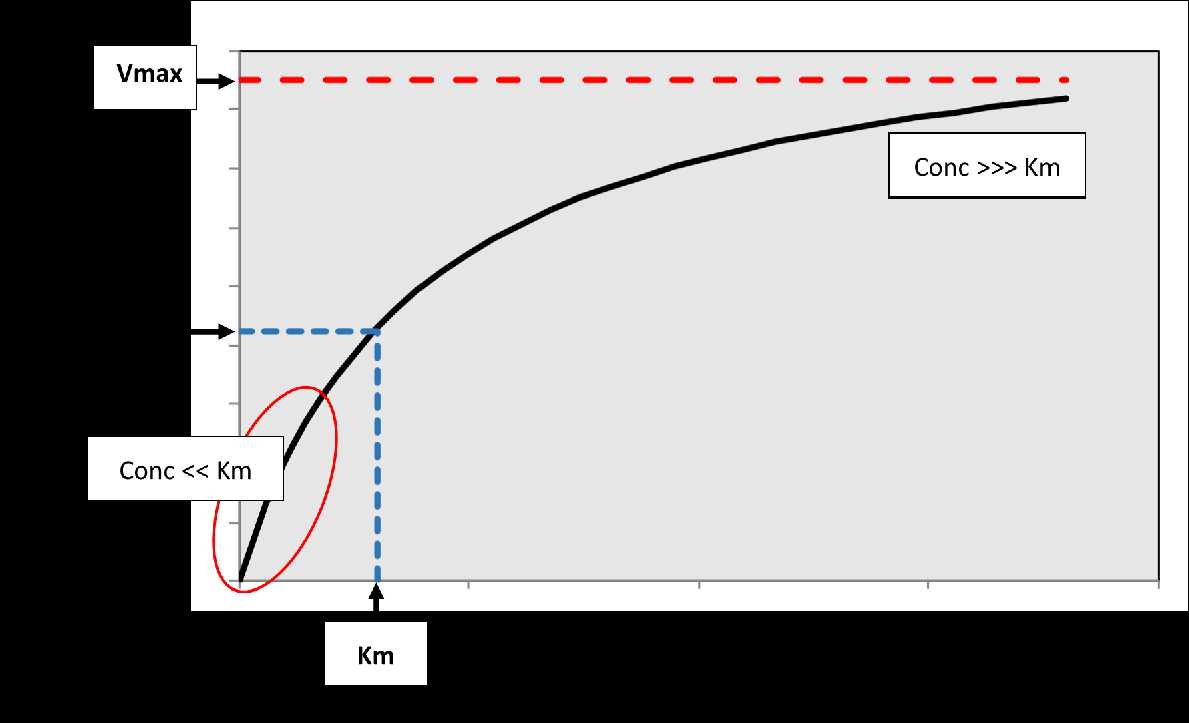
Figure
2. The relationship between substrate
concentration and rate of the reaction. Vmax is the maximum velocity of
the
reaction, while Km corresponds to the concentration associated with 50%
Vmax.
At low concentrations relative to Km, a linear relationship exists
(first-order
kinetics) indicated by the red oval on the plot where rate
proportionally
increases with concentration. At very high concentrations relative to
Km, the
curve plateaus so that the rate of the reaction becomes constant and
independent of concentration (approximates zero-order kinetics).
Most
drugs display first-order
(also called linear) elimination because the concentrations encountered
clinically are well below their Km. Nonlinear
elimination at one
organ does not imply elimination via other process must also be
nonlinear. The
relative contribution of elimination pathways may differ with
concentration. The
elimination rate by one pathway may become saturated while another
elimination
rate continues to increase linearly with concentration, making it the
dominant
driver of drug disposition at higher concentrations.
Nonlinearity
in elimination has
been described here for metabolic processes, as may be seen for drugs
such as
phenytoin or ethanol, but may also result from other processes.
Rifampicin
displays nonlinear elimination in part due to saturation of biliary
excretion
and due to autoinduction of its metabolising enzymes over the first
weeks of
therapy. Saturation of active secretion by renal tubule transporters
causes
nonlinear elimination of dicloxacillin. Monoclonal antibodies typically
display
nonlinear elimination due to target-mediated binding dominating
kinetics at low
concentrations. Elimination processes can be described using mixed
models for
linear and nonlinear clearance. This has been done for ethanol (see http://holford.fmhs.auckland.ac.nz/research/ethanol)1
and itroconazole (simulation
available at https://acp-unisa.shinyapps.io/Itraconazole_PopPK_Model/)2.
Differential
equation
solvers
Simple models may be solved
analytically. That is to say, an
algebraic solution exists and that solution may be solved exactly. An
example
of an analytic solution for a one compartment model is
| C(t) = Dose/V * exp(-CL/V * t) | Equation 7 |
More complex models, like the type
encountered often in
pharmacokinetics where two or more compartments exist, may be too
complex to
solve analytically. The solution may not be known, or it be known but
be too
complicated for most purposes. An alternative is to solve numerically
using
numerical integration of differential equations. When using
differential
equations, a series of equations is written each explaining the change
in a
variable over time for each part of the system. In pharmacokinetics the
variable of interest is usually drug concentration, and the parts of
the system
are the compartments of the body (e.g. central, fast equilibrating
peripheral,
slow equilibrating peripheral). A differential equation solver is used
to
estimate the change in the variable over small steps in time (t + dt,
where dt is the step in time, or the
interval).
dt is usually set at some small
amount; the smaller it is, the more accurate the solution but the
longer the
integration process takes. Integration methods differ in the way they
estimate
the change in the variable at each step in time. Numerical integration
of
differential equations gives an approximate solution as opposed to an
exact
one.
Euler’s method
Euler’s method is the simplest
approach to solving
differential equations. The slope of a tangent line gives the
instantaneous
rate of change at that moment. Euler’s method uses very small steps in
time (dt) to approximate the slope
of the
time-concentration curve for each compartment using the following
equation:
| C(t + dt) = C(t) +dC/dt * dt | Equation 8 |
where Ct is
the concentration at the last time
step.
Euler’s method is easy to implement
but dt must be very small to ensure
accuracy is
retained. Its use is limited in pharmacokinetics because this makes it
slow to
integrate for common clinical problems. The large number of steps
needed also
results in high rounding errors during computing (or ‘round off’
errors).
Runge-Kutta method
The Runge-Kutta method 4 is commonly
used because it
provides a good trade-off between accuracy and speed. The Runge-Kutta
method 4 approximates
the change in concentration at each step using a weighted average of
four
increments within the time step: the beginning of time interval dt, the midpoint of dt,
a second estimate of the midpoint of dt,
and the end of dt
interval. Unlike Euler’s method (which is sometimes referred to as
“First Order
Runge-Kutta”), step sizes can be larger without compromising on
precision.
Many other methods of numerical
integration for differential
equations exist.
References
1. Holford
NH. Clinical pharmacokinetics of
ethanol. Clinical pharmacokinetics. 1987;13(5):273-292.
2. Abuhelwa AY, Foster DJR, Mudge S, Hayes D, Upton RN. Population Pharmacokinetic Modeling of Itraconazole and Hydroxyitraconazole for Oral SUBA-Itraconazole and Sporanox Capsule Formulations in Healthy Subjects in Fed and Fasted States. Antimicrobial Agents and Chemotherapy. 2015;59(9):5681-5696.
Workshop hints
Note: All files should be loaded from and saved to your Pharmacometrics Data\Non-linear PK folder for this assignment. You may find it useful to create a separate folder for each program inside the Non-linear PK folder as you will create several files during this assignment.
Some hints (shown in grey boxes) refer to changes needed for subsequent problems.
You may find it easier to read this page if your click on the "[Hide Side Menu]" text at the top
Excel
Find the file Pharmacometrics Data\Non-linear PK\ka1_mo.xlsm
- Open ka1_mo.xlsm with Excel. Note this is a macro enabled file. You should enable content so you can use the macros.
- Look at each of the 3 worksheets (ka1_mo, ODE_ka1, ODE_bo1).
- Identify:
- The model equation. You will need to modify the Excel Options Customize Ribbon to show the Developer tab on the Ribbon. Once this is completed, view the Visual Basic editor by either clicking on the Developer tab then on Visual Basic, or using the shortcut Alt-F11. Click on the ka1_mo.xlsm Module and open mODEFunctions. Look for the Ethanol_KA1 function.
- The model parameters
- The independent variable
- Export the simulated data from the ka1_mo worksheet in ka1_mo.xlsm to a format that other programs can read using the following steps
- Create
a new Excel workbook to make a data file from the ka1_mo worksheet.
Add the following headings in the top row of the data file. It
is important to put the # before ID so that the file can be
used
for NONMEM. The CONC column name represents the Dependent Variable
(i.e. the
observation).
#ID TIME AMT DVNote: Monolix will use these header names but NM-TRAN does not use them.
- Fill the data file #ID column down to row 14 with the value 1. Copy the values from column E in the ka1_mo model worksheet into the data file TIME column. Copy the concentrations from column F (simulated observations) in the ka1_mo model worksheet into the data file DV column. Insert a row below the header row. Set the TIME to 0 and the DV to missing ("."). Enter the dose used for simulation in the AMT column in this row. Set the AMT in all the other rows to missing (".").
- Now save the data file using 'Save As' and choose CSV (Comma delimited, *.csv) format.
- Save in your Pharmacometrics Data\Non-linear PK folder.
- Name the file ka1_mo_40g.csv (Be careful -- use ka1_mo_40g.csv NOT ka1_m0_40g.csv, i.e. oh NOT zero).
Important: use Paste Special Values rather than a simple paste to prevent the formulae in column F being copied to the data file.
The data file for the bo1 model should look like similar to Table 1, but your DV values will be different.
| #ID | TIME | AMT | DV |
| 1 | 0 | 40 | . |
| 1 | 0.1 | . | 50.4 |
| 1 | 0.3 | . | 122.4 |
| 1 | 0.5 | . | 182.3 |
| 1 | 0.7 | . | 224.1 |
| 1 | 1 | . | 258.4 |
| 1 | 1.5 | . | 266.7 |
| 1 | 2 | . | 262.2 |
| 1 | 2.5 | . | 213.8 |
| 1 | 3 | . | 153.0 |
| 1 | 4 | . | 51.2 |
| 1 | 5 | . | 9.6 |
| 1 | 6 | . | 3.4 |
| 1 | 7 | . | 1.6 |
-
Table 1. Data file for ka1_mo_40g.csv
Berkeley Madonna
- Open the Berkeley Madonna shortcut in the folder "Pharmacometrics Programs".
- Add code to the Equations window defining the STARTTIME, STOPTIME, integration stepsize (DT), the output interval (DTOUT), the model parameters and the model equation (code shown in Figure 1 for the ka1_mo model).
- Click on Run to run the model.
- Save your model with the name ka1_mo.mmd (in your Pharmacometrics Data\Non-linear PK\Madonna folder).
- View a table of times and concentrations by clicking on the Table icon in the Run 1 graph window.
STARTTIME = 0
STOPTIME=12 ; h
DT = 0.02
DTOUT=0.1
dose=40 ; g ethanol (batch parameter 0.1 g->1000 g shows first-order to zero-order)
vmax=10 ;g/h
km= 80 ;mg/L
v=35 ; L
tabs=1; h
ka=logn(2)/tabs
vmaxmg=vmax*1000 ; g/h -> mg/h
init(gut)=dose*1000 ; g -> mg
init(amt)=0 ; g -> mg
C=amt/v
ratein=ka*gut
d/dt(gut)= -ratein
d/dt(amt)= ratein - vmaxmg*C/(km+C)
Figure 1. Code for ka1_mo.mmd (Berkeley Madonna)
Monolix
- Open the Monolix shortcut in the folder "Pharmacometrics Programs".
- Click on the 'New Project' block.
- In Monolix, click 'Data' and use 'Browse' to locate your ka1_mo.csv file. This can be done by copying the path to the folder from Windows Explorer into the Monolix "Load data file File name:" box. e.g. P:\My Pharmacometrics\Pharmacometrics Data\Non-linear PK
- Select ka1_mo_40g.csv and click 'Open'. The data information window will appear.
- Monolix should identify that your input file has a header
row and your data should appear under the headings: _ID TIME AMT DV.
Click "Accept" and then click "Next".
You can select the type of data associated with the headings manually by clicking the drop down menus. If the independent variable is not TIME then select REGRESSOR for the type.
- Instead of using the model library, we will use MLXTRAN with the ka1_mo model. Start by opening a text editor (e.g. Editplus) and enter the code shown in Figure 2.
- Save the model as ka1_mo_mlxt.txt in a Non-linear PK\Monolix folder.
- Click on 'Structural Model' then "Browse" and navigate to
your "Non-linear PK"
folder'. Select ka1_mo_mlxt.txt and click 'Open', then
'Accept'.
If you get a compile error double check that your code is identical to that shown in Figure 2 and be sure to press ENTER after the last line of code - this is required to 'end' the last statement.
- Change the initial parameter estimates under "Check Initial
Estimates" to those used in the ka1_mo simulation. A plot of
predictions
based on the model and initial parameter estimates will display along
with the observed values.
- Click on "Statistical Model and Tests".
- Click on the small circle in the blue boxes to enable "Population Par", "Standard Err" and "Plots".
- Click on the grey bar next to the blue part of "Plots" and click to enable "Observed data", "Individual fits" and "SAEM". Disable all other options. Close the Plots options window.
- In the "Observation Model" section choose the "Error Model" called "COMBINED1" from the drop down list.
- In the "Individual Model" section click on "None" for
"Random Effects"
Because these are data from a single individual, there is no between subject variability (random effects). The SD of random effects is therefore 0.
- IMPORTANT: Save the project as ka1_mo_project.mlxtran in your Non-linear PK\Monolix folder before trying to "Run" the model.
- Estimate the parameters by clicking on 'Run'. This will take a while depending on the complexity of the model. During the estimation process you can see how the parameter estimates are being changed and settle down towards the final value.
- When the estimation finishes close the Monolix Scenario window.
- Click on 'Plots' and look at the individual fit. Use the "Display" options to show "Predicted Median" and "Prediction Interval" for the "Individual predictive check". You can alter the names of plot axes using the 'Axes' tab. When you are ready, you can export all of your plots into your ka1_mo project folder using the 'Export' tab on the main menu.
- View the parameter estimates by clicking 'Results'. A text file containing these results is saved in a 'pop_parameters.txt' in the ka1_mo project folder.
- Save the project as ka1_mo_40g_project.mlxtran in your Non-linear PK\Monolix folder.
Ethanol disposition
The administration of ethanol is via an oral bolus
The modelled entity is CC (central compartment ethanol).
The only output is CC
[LONGITUDINAL]
input={V, Vmax, Km, Tabs}
PK:
depot(target=gut, p=1000) ;p=transforms the dose g into mg
EQUATION:
odeType=stiff
;Parameter transformation
Vmaxmg=Vmax*1000 ; g/h -> mg/h
Ka=log(2)/Tabs
;Initial conditions
t_0 = 0
gut_0 = 0
amt_0 = 0
ratein = Ka*gut
CC = amt/V
;Ordinary Differential Equations
ddt_gut = -ratein
ddt_amt = ratein - Vmaxmg/(Km+CC)*CC
OUTPUT:
output={CC}
IMPORTANT: MLXTRAN is case sensitive. Take care to be consistent with upper and lower case names.
NONMEM
- Open the NONMEM shortcut in the folder "Pharmacometrics Programs".
- Change directory to the Non-linear PK folder by
typing this command in the NONMEM window then press
<ENTER>.
cd NONMEM
You could also change to the NONMEM directory using the change directory command as follows: cd NON followed by pressing Tab. This is because NONMEM only needs the first unique letters of the folder name to distinguish the folder you are referring to within the directory.
- Make a NONMEM directory by
typing this command in the NONMEM window.
md NONMEM
You only have to make the directory once.
- Change to the NONMEM directory from the Non-linear PK
directory.
cd NONMEM
- Use the Windows Notepad (or EditPlus) to create the
following code in a file named ka1_mo_40g.ctl e.g. by using the
command:
notepad ka1_mo_40g.ctl
- Enter the code for ka1_mo_40g.ctl shown in Figure 3.
$PROB ethanol disposition
$INPUT ID TIME AMT DV
$DATA ..\..\ka1_mo_40g.csv
$EST METHOD=COND NSIG=3 SIGL=9 MAX=9990 PRINT=1
$COV
$THETA
(0,10,) ; POP_VMAX g/h
(0,80,) ; POP_KM mg/L
(0,35,) ; POP_V L
(0,1,) ; POP_TABS h
$OMEGA
0 FIX ; PPV_VMAX
$SIGMA
0.01 ; RUV_PROP
0.25 ; RUV_ADD mg/L
$SUBR ADVAN13 TOL=9
$MODEL
COMP=(GUT)
COMP=(CENTRAL)
$PK
VMAX=1000*POP_VMAX*EXP(PPV_VMAX) ; g/h -> mg/h
KM=POP_KM
V=POP_V
TABS=POP_TABS
KA=LOG(2)/TABS
F1=1000 ; g -> mg
S2=V
$DES
GUT=A(1)
CC=A(2)/V
RATEIN=KA*GUT
DADT(1)= - RATEIN
DADT(2)= RATEIN - VMAX/(KM+CC)*CC
$ERROR
CONC=A(2)/V
Y=CONC*(1+RUV_PROP)+RUV_ADD
$TABLE ID TIME Y
ONEHEADER NOPRINT FILE=ka1_mo.fit
Figure 3. NM-TRAN code for ka1_mo_40g.ctl (NONMEM)
The $OMEGA parameters are FIXed to 0. This is because there is only one individual being modelled. These random effects parameters are used to describe between subject variability when there is more than one individual.
- Save the file. Check using Windows Explorer that you can find the file "ka1_mo_40g.ctl" in the Non-linear PK\NONMEM folder.
- The data file name must match in the $DATA record
of the bo1.ctl file.
In order for NONMEM to find the data file the $DATA record has to include a path relative to the folder where NONMEM is executed. This is only needed if the data file is not in the same folder as the control stream. In this case the data file is in the folder above the folder with the control file therefore the relative path is required to find the data file.
- Execute NONMEM with this command in the NONMEM window:
nmgo ka1_mo_40g
When you get errors from NONMEM with the nmgo command then please read the error message carefully and try to understand what it is telling you. The usual errors that occur with these example problems will give you some clues to what you might need to change in your ctl file.
Commands can be recalled by using the Up arrow on your keyboard. You can easily repeat the command without more typing or edit it to save the amount of typing you do.
- Use
the Windows Notepad or EditPlus to open and look at the saved
results in the '.smr' file. The results are saved in a folder with the
same name as the ctl file but with the extension '.reg' e.g. use the
following command or open the file using the Windows Explorer.
notepad ka1_mo_40g.reg\ka1_mo_40g.smr
- Create a plot of TIME versus Y (predicted conc) and DV (observed conc) using the ka1_mo_40g.fit file in the ka1_mo_40g.reg results folder.
- You
can open your fit file directly in Excel by right clicking on the file
and selecting “Open With” and then “Excel”. You need to reformat the
Excel file in order to see its contents. You can do this using steps
13-15 below.
If you are unable to open the fit file in this manner, open an Excel window and click “Open” and “Browse” to to navigate to open the NONMEM .reg folder fit file. You will need to select the option “All files (*.*)” at the bottom of the window. This will allow you to see all files regardless of their extension. Select the .fit Excel file. You need to reformat the Excel file in order to see its contents. Use the Text Import Wizard to reformat the Excel file (you can skip step 13 below if you use this option).
- Select column A then click on the "Data" menu item then click on "Text to Columns". Click on "Finish". This will separate the values into separate columns.
- Select all cells in the worksheet (e.g. press ctrl-A) then right click on a cell and click on "Format cells". Click on the "General" option. This will make the numeric values easier to read.
- Delete row 1 which contains the value "TABLE 1".
- Create a graph of TIME versus Y (predicted conc) and DV (observed conc).
- Make sure you save your changes as a new .xlxs file so that your changes are preserved.
Learning
- Show a graph of the Excel simulated data for each model.
- What do the model parameters mean?
- What are the kinds of experimental data they might be used to describe?
- Repeat either the Monolix or NONMEM steps using a 10 g dose instead of a 40 g dose in the ka1_mo.xlsm ka1_mo worksheet. Be sure to use a different file name for the data file, Monolix project and NM-TRAN control file e.g. ka1_mo_10g.csv, ka1_mo_10g.mlxtran, ka1_mo_10g.ctl.
- Compare the results with a 10 g dose and a 40 g dose. Describe any differences in the final parameter estimates and standard errors (if available). Try to provide an explanation for any differences you find.

